データのコレクションにおけるパーセント誤差は、元の値と比較した正確な値と近似値の差です。このパーセント誤差はパーセンテージで表現されるため、100 倍されます。
パーセント誤差は、絶対誤差または相対誤差として表現できます。機械の精度誤差、計算誤差、測定誤差、環境条件などにより誤差が発生する場合があります。
エラーの割合は、分析中にエラーがどの程度重大であるかを判断するのに役立ちます。パーセント誤差がより小さい場合は、元の値に近いことを意味しますが、パーセント誤差がより大きい場合は、実際の値と近似値との間にかなりの差異があることを意味します。
たとえば、2% の誤差は元の値に非常に近いことを意味し、56% の誤差は実際の値と近似値の間に大きな差があることを意味します。
測定中に手が震えたり、機器が故障したり、材料が正確でなかったりする可能性があるため、測定中の誤差は蔓延します。
![エラー率の計算方法 [+3 ツール]](https://popinsight.jp/wp-content/uploads/2020/11/Testingtime11.png)
パーセントエラーの計算
パーセント誤差を計算するには、2 つの使用可能な値が必要です。 1 つは正確な値、2 つ目は近似値です。これらの値を両方とも減算し、元の値で割ります。パーセント誤差はパーセントの形式で表現されるため、受け取った数値に 100 を掛けます。つまり、パーセント誤差は相対誤差に 100 を掛けたものになります。
誤差の割合 = [(実際の値 – 期待値) / 期待値] × 100
式の構成要素
実際の値: 実際の値は、特定の読み取り値の数値を示します。実際の値は読み取り時に記録されるべきでしたが、いくつかのエラーのため、この値を記録できませんでした。これは、計算を実行するのに理想的な一般的な値です。
期待値: 期待値は、実験中に記録された読み取り値を示します。ほとんどの場合、誤差により実際の値とは異なります。エラーの原因としては、機械のデフォルト、読み取り時のエラー、または空気や機器の故障や破損などの環境要因が考えられます。
いくつかの例
例1
少年が三角形の面積を測っていたところ、その測定値は 462 平方センチメートルだったそうです。ただし、正方形の元の面積は 465 平方センチメートルです。パーセント誤差を計算します。
解決
測定面積の値 = 462 平方センチメートル
実際の面積の値 = 465 平方センチメートル
計算
実際の値 – 測定値の差: 465-462 = 3
したがって、3 は測定誤差です。
誤差を実際の値で割ります – 3/465 = 0.00645
得られた値に 100 – 0.00645 X 100 = 0.64% を掛けます。
したがって、三角形の面積を計算する際のパーセント誤差は 0.64% です。
例 2
あなたがパーティーを計画していて、推定 20 人がパーティーに参加する予定だったのに、なんとか参加できたのは 18 人だけだったとします。推定の誤差パーセントを計算します。
解決
当初の予定人数 = 20
来た人=18人
計算
実際の値の差 – 最終値 = 20 – 18 = 2
つまり、2 がここでのエラーです。
誤差を実際の値で割ります – 2/20 = 0.1
値に 100 を掛ける – 0.1 X 100 = 10%
したがって、ゲスト数の推定における誤差の割合は 10% になります。
例 3
水の沸点を測定する実験を行ったところ、実験中に結果が 102℃ であることが判明したとします。水の実際の凝固点は100℃です。
解決
水の実際の沸点 = 100°C
記録された水の沸点 = 102°C
計算
実際の値と計算値の差 = 100 -102 = 2°C (パーセント誤差を負にすることはできないため、正のみに保ちます)。
つまり、2 がここでのエラーです。
誤差を実際の値で割る – 2/100 = 0.02
得られた値に100を掛ける – 0.02 X 100 = 2%
したがって、水の沸点測定におけるパーセント誤差は 2% です。
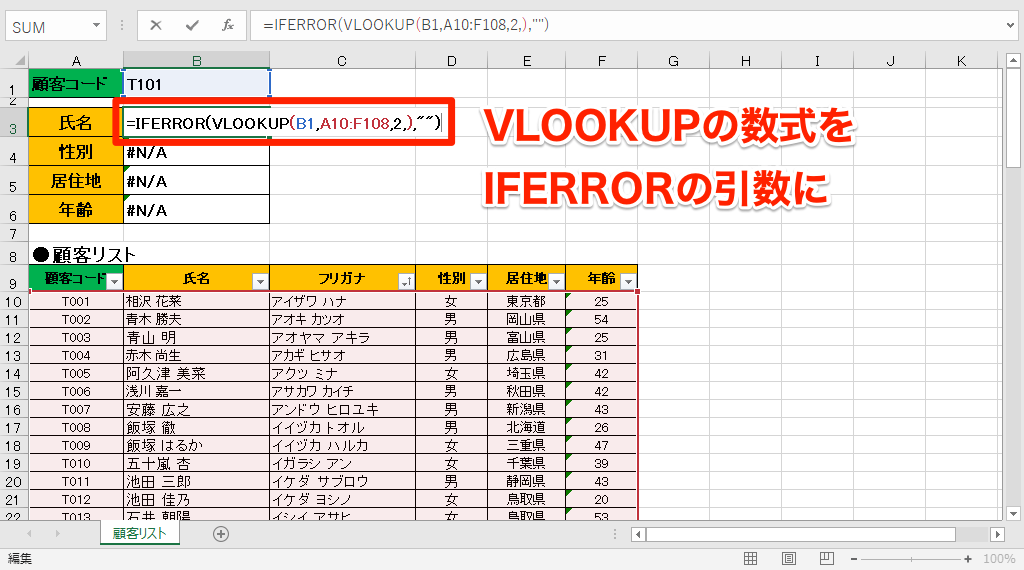
![エラー率の計算方法 [+3 ツール]](https://kokodane.com/gazo2013/kan/iferror.png)
誤差率が重要な現実のシナリオ
- エラー率は、完了した特定のタスクが基準を満たしているかどうかを判断する上で重要な役割を果たします。自分の間違いを指摘するのに役立ちます。
- パーセント誤差は、わずかな誤差も許容されない実験室の手順や大規模産業で役立つ場合があります。
- パーセントエラーは、大量の注文を完了する必要があり、その完了にはいかなる誤差の範囲も存在しない場合にも使用されます。
- 科学実験室では、エラー率の使用が重要です。
パーセント誤差と絶対誤差
測定における絶対誤差は、実際の値と計算値の差です。基本誤差の単位は初期値と同じです。
例
あなたが 2 kg のマンゴーを購入する予定だったのに対し、店主が 1.98 kg を測ったとします。この場合、絶対誤差は 2 – 1.98 = 0.02 になります。
一方、パーセント誤差は、絶対誤差を元の値で割り、得られた答えに 100 を掛けることによって計算されます。パーセント誤差は単位のない量です。
上の例では、 絶対誤差 は 0.02 です。
次に、パーセント誤差を計算するために、それを 20 で割ります。
0.02/20 = 0.001
したがって、この場合の パーセント誤差は 0.001 X 100 = 0.1% となります。
パーセント誤差と相対誤差
あらゆる計算における相対誤差は、絶対誤差を実際の値で割ったものです。これは、パーセント誤差が真の値と観測値の差を実際の値で割ったものであることを意味します。
例
天気予報では今日の気温は38度だった。しかし、温度は42℃まで上がりました。
まず、2 つの数値の差、つまり期待値と実際の値を求めます。
42° – 38° = 4°C
次に、 相対誤差 を計算するために、この数値を実際の数値、つまり 38°C で割ります。
4/38 = 0.1052
一方、 パーセント誤差は、相対誤差に 100 を乗算したものです 。
上の例では、パーセント誤差は 0.1052 X 100 = 10.52% になります。
さて、パーセント誤差、相対誤差、または絶対誤差を計算するのは非常に簡単であることがわかるでしょう。
いくつかのオンラインパーセント誤差計算ツールを利用すると、パーセント誤差の計算を簡単に行うことができます。これらの計算機がすべてを自動的に実行してくれるため、パーセント誤差の計算方法に迷う必要はありません。
誤差計算ツール
#1. 電卓スープ
計算スープは、 実験値と実際の値の間の誤差のパーセンテージを計算するのに役立ちます。あなたがしなければならないのは、値を入力して結果を待つことだけです。電卓はすべての計算を単独で実行し、正確な結果を提供します。
このページには 2 つの異なる列が表示され、そこでパーセント誤差を計算したい数値の値を入力し、残りの計算を電卓に任せます。
#2. 電卓.net
Calculator.net に は 2 つの列があり、実際の値と推定値を入力し、残りの計算を電卓に任せます。これは、計算したいデータのサンプルが大量にあり、すべてのケースで誤差のパーセントを手動で計算する時間がない場合に便利です。計算機を使用するとプロセスが簡単になり、あまり遅れずにすぐに答えが得られます。
パーセント誤差は避けられません。値を下げることしかできませんが、パーセント誤差の読み取りがゼロになることは発生しません。ほぼゼロになることはありますが、正確にゼロになることはありません。
#3. 優れた電卓
多くのオンライン計算機は、パーセント誤差の問題を解決するのに役立ちます。これらの中で、最も便利なものの 1 つは Good Calculator です。この計算機では、推定値と元の値を入力するだけで、自動的に結果が表示されます。
膨大な計算を実行する手間が省け、時間を節約できます。包括的な計算を数秒以内にすばやく解くことができ、時間を大幅に節約できます。

したがって、大量のデータが手元にあるものの時間がない場合、計算機はパーセント誤差を計算するのに最適です。
結論
計算に誤りがあると、プロジェクトや研究が完全に台無しになる可能性があります。ここで、オンラインのエラー率計算ツールを利用して、人的ミスを発生させずに作業をより効率的に行うことができます。
金融に興味がある場合は、これらの利益率計算ツールをいくつか見てみるとよいでしょう。






![2021 年に Raspberry Pi Web サーバーをセットアップする方法 [ガイド]](https://i0.wp.com/pcmanabu.com/wp-content/uploads/2019/10/web-server-02-309x198.png?w=1200&resize=1200,0&ssl=1)


![アジャイル ソフトウェア開発で使用される最も人気のある 9 つのツール [2023]](https://i2.wp.com/www.nilab.info/lab/twitterpic/1513065310315708416_1.jpg?w=1200&resize=1200,0&ssl=1)


